To find the eigenvalues, we solve the equation
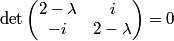 Evaluating the determinant, we have 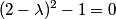 So, the eigenvalues are both 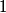 and and 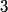 . Therefore, answer (B) is correct. . Therefore, answer (B) is correct. |
To find the eigenvalues, we solve the equation
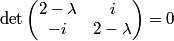 Evaluating the determinant, we have 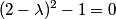 So, the eigenvalues are both 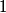 and and 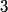 . Therefore, answer (B) is correct. . Therefore, answer (B) is correct. |